概要

研究游戏中对目标追捕，重要的是选择一条合适的路径，让追逐者去按照找到的路径去追捕。随着目标的不断移动，只要我们不断的更换路径的终点坐标，最后就能成功的追捕到移动的目标。所以归根结底的说我们要实现对移动目标的追捕首先也是最重要的就是研究如何找到一条最优的路径，即研究寻径算法。

一概述

常用的地图寻径算法有状态空间探索(State Space Search—ing)和启发式搜索。算法中需要解决的最基本问题是如何避开障碍物，因此，在介绍地图寻径算法之前，先简要说明一下游戏中地图的文件结构及其相关概念。

1.1 游戏地图

在游戏软件中，地图一般是由一块块小的方格图片拼接而成的，组成地图的图片元素被称为“瓷砖”。地图编辑器将瓷砖按一定的规则“铺”成一张完整的地图，并将地图组成规则保存在一个文件中，此文件被称为地图文件。游戏软件运行过程中，当切换到某个场景时，首先需要读取地图文件，其次按文件所提供的数据，在地图方格内放入相应的瓷砖，最后把铺好瓷砖的游戏地图显示在屏幕上。精灵在地图上行走时，应随时判断周边的瓷砖是否可通，以便计算出下一步行走路线。一般情况下，一幅编辑好的游戏地图中瓷砖有两种状态，即可通和不可通，如图1所示。

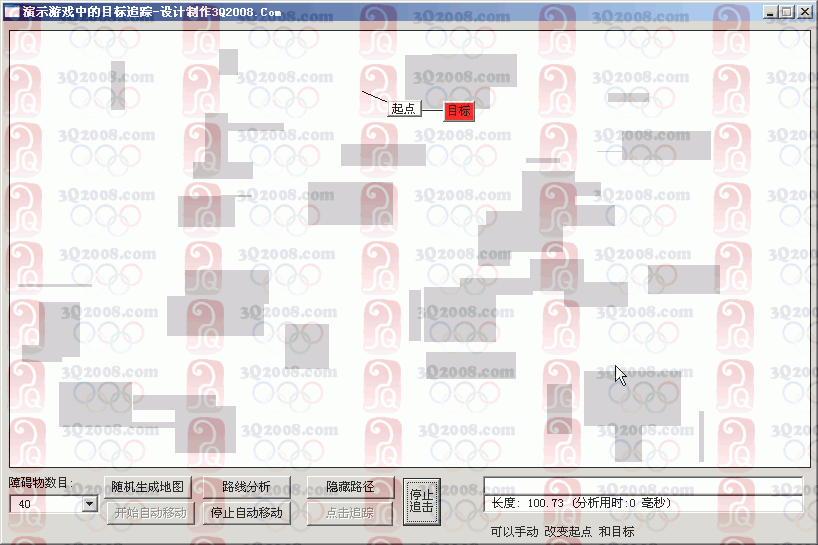
二 A*算法

基于几种寻径算法的性能和可适用性，我选择了启发式搜索进行研究。因为它是人工智能在游戏开发方面的应用，比前两者更能提高效率和节省空间。而A*寻径算法更是启发式搜索中最经典的算法，是当前大多数RTS游戏开发者的首选。下面让我们认识一下A*寻径算法。

2.1. 了解A*算法的基本原理

在这里我们将基于一个实例去研究A*算法。

定义搜索区域：

如图的砖块型游戏中。黑色代表障碍物，点代表节点，即可以行走的地方。搜寻的路径起点是蜘蛛所在节点，重点是人类所在节点。

2.2.A*算法的总结

通过上面对A*算法的简介，我们对A*算法进行分析。A*算法的核心是一个估价函数：f(x)=g(x)+h(x)，它是对从初始状态S₀经过当前状态x到达目标状态S的整个路径的估计长度。其中g(x)是对已走距离的估计函数，h(x)是对当前状态到目标状态距离的估计。在A*搜索过程中，用整个路径的估计长度对部分路径进行排序，每次选择具有最短估计长度的部分路径进行扩展。

如果评估函数f能够准确反映实际路径长度，则能使搜索限定在最短路径上。但是，评估函数是关于路径长度的预期，这种预期值不一定准确。公式的第一部分，是利用已经得到的信息计算出来的，可以认为是准确的；第二部分是对到达目标结点所余下路径长度的估计值，往往不准确。这种误差对搜索选择有很大影响。为了保证能得到最优路径，A*算法要求对长度的估计值低于实际长度。此时，实际长度是评估函数的上限。这样当找到一条到达目标结点的路径时，若它不是最短的，则存在估计长度更小的路径可以扩充。

因此，A*算法要求h(x)≤h*(x)，其中h*(x)是当前状态到目标状态距离的准确值。

2.3 算法的实现步骤

从起点开始，首先将其放入未扩展节点表(OPEN表)中，同时放入起点到达目标点的预计代价，预计代价依启发值而定，通常，启发值取两个节点之间的几何距离，随后，重复以下循环直

至OPEN表为空。

(1)从OPEN表中取出到达目标点具有最小预计代价的节点；

(2)如果所在节点已为目标点，则结束循环；

(3)如果所在节点不是目标点，则检查与此节点周边的8个新节点；

(4)对于每个可通的节点，计算穿过该节点到达目标点的路径的预计代价(预计代价=从起点到达该节点的实际代价+从该节点到达目标点的预计代价)；

(5)将周边可通的所有节点均加入到OPEN表中，返回至第(1)步。

由A 算法所选得的路径上的节点(包括起始点及目标点)被称为关键点，由关键点所构成的路径就是所求的最短路径。

无法找到演示,请联系客服

点击联系客服


∷下载地址∷	∷相关毕设∷
下载地址一无需注册演示程序直接下载

概要

一 概述

1.1 游戏地图

二 A*算法

2.1. 了解A*算法的基本原理

2.2.A*算法的总结

2.3 算法的实现步骤

一概述